Océzo, des makers 2.0, pour retaper & coder
The "Garbage / Earth bag" project
$\hspace{100px}$
 $\hspace{100px}$
$\hspace{100px}$
When I was a kid, I loved hiking in the forest of Poligny
with my family near Nemours, France. My mother used to bring a trash bag with her. So she often ended the walk by picking up the rubbish near picnic areas.
That was in the 80s, far before the "plogging" fashion. It marked me a lot.
Years after, I had the incredible privilege to visit Polynesia in 1999. I was in "classes prépa" and I discovered that Paradise existed on Earth...
This was a real shock. But I also discovered that in Bora Bora
the diving spot of the famous "manta rays" was just near the landfill of this iconic island.
No tourist tour mentions that horrible truth. That was another shock.
Years after again, my wife and I travelled to the beautiful island of Phu Quoc
for our honey moon in 2018. Mass turism is already wildly developed there and I could not help but pick up garbage in front of some paradisiac beaches.
This time it was my mother-in-law who had a shock. She was ashamed to see her step-son picking-up the waste. And she begged me to stop.
I fully understand. I never knew war and poverty.
However, next year I have recidivated in front a "romantic" paysage near Nha Trang,
already stained with plastics and abandoned to the fate of the poorest to burn the rubbish at night.
Once again my Vietnamese neighbors were shocked to see me picking up the garbage. They explained me that they did not know what to deal with the scale of the problem.
They live in megacities and I know they have to struggle to live.
So here's my idea. The aim is to pay the people who pick up the garbage, especially the poorest, thanks to trash bags with QR code
and a robust smartphone application. I know it's not perfect. But for the moment, that's the best I can think of. My background aim is to speed up the awareness of the local public powers.
Which must go through more taxes, taxes to the industrial process of course. This is what is called "regulation", in the name of the "public interest". The Chinese would say harmony.
For the moment, I just draw a cartoon to explain how it could work. So please excuse the "not yet finished / on going" (and french! :$) work. I never developed an Android / iOS application.
I'm just a C/C++/Matlab/Python/Computer Vision/Robotics guy. But I'm sure that it's "achievable". So that's why I released this idea today.
I hope that you will find it "great". Because, to be honest, my drawings were done in may, during my last hollidays, and now, they took the dust in Paris...
You know, I have a family, I have a work, and time is running too fast... Some experts say that we can't wait for 10 more years...
That's why I answered to Bertrand Piccard's call through his foundation Solar Imulse for the 6th of November. So if you are interested (Jeremy Grantham, can you hear me!?) to finance / label this idea, if you work for Veolia, or if you just find it great, don't hesitate to contact me (just put "[Earth bag]" in the header or your email please).
Thanks in advance for your support.
Jean-Marc
Scanner 3D
Avec Julien, Brigitte et Baptiste de LFdQ et AcoLab nous comptons fabriquer un petit
scanner 3D fait maison.
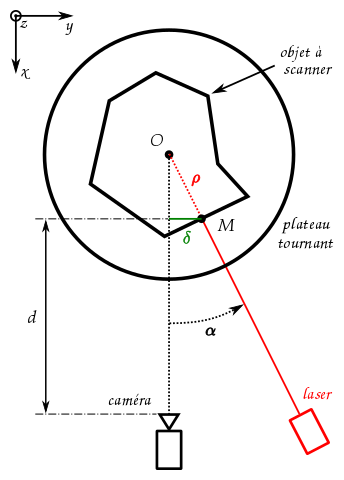
De nombreuses possibilités existent mais la plus simple est d'utiliser un laser avec une caméra. Le principe est de projeter
un motif connu sur l'objet, une ligne verticale ici, et de mesurer sa déformation dans l'image. On parle de reconstruction
par "lumière structurée". Le laser, l'objet et la caméra forment alors un triangle (voir la vue ci-dessous) et le décalage
$\delta$ de la ligne, mesuré dans l'image, dépend de l'angle $\alpha$ (entre la caméra et le laser) et de la distance
$d$ (entre la caméra et l'objet). Par la suite $\alpha$ sera maintenu constant.
$\hspace{220px}$
 $\hspace{188px}$
$\hspace{188px}$

$\hspace{246px}\alpha = 0$ $\Rightarrow$ $\delta = 0\hspace{212px}\alpha \neq 0$ $\Rightarrow$ $\delta = f(\alpha, d)$
Pour obtenir des points sur tout l'objet le mieux est de le placer sur un plateau tournant. En effet, pour chaque point M de la
surface il est plus facile de remonter au rayon $\rho$ qu'à la distance $d$ (cf. schéma ci-dessous). La solution tient alors en
une petite formule de trigo ($\alpha=cst$) :
\[ \rho = \frac{\delta}{sin (\alpha)} \]
$\hspace{78px}$
 $\hspace{110px}$
$\hspace{110px}$
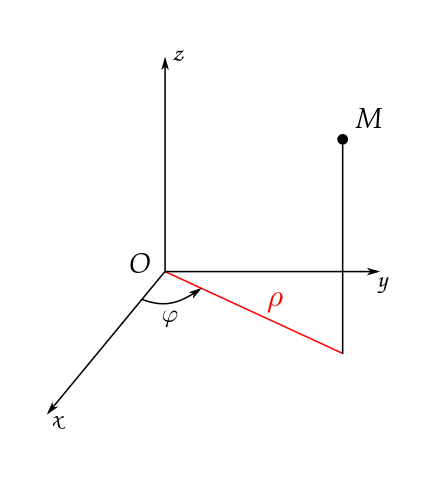
En notant $\varphi$ l'angle du plateau, les coordonnées du point $M(x,y,z)$ dans le repère fixe s'écrivent :
\[ \left\{ \begin{array}{l}
x = \rho . cos(\varphi) \\
y = \rho . sin(\varphi) \\
z = z^{'}
\end{array} \right. \]
Ainsi, après $n$ coupes et différents filtrages (points à l'$\infty$, artefacts...) on accumule une liste de points 3D plus ou
moins fidèles. Il reste à la mettre en forme pour pouvoir exporter un fichier 3D standard :
STL,
OBJ ou
PLY (ASCII ou binaire). Voilà. Bien sûr, il reste beaucoup de travail
pour reproduire la pièce à l'identique mais c'est un début. Pour information, il existe encore d'autres motifs de lumière structurée
(grille alétoire de points en IR pour la
Kinect, bandes d'épaisseurs variables chez
David-Laser, etc.). Ces derniers améliorent
sensiblement la résolution mais leurs traitements s'avèrent bien plus complexes. Nous les aborderons dans un second temps.
Finir ma thèse...
J'ai démarré une thèse de vision par ordinateur en 2009. L'objectif était de poursuivre une zone d'intérêt à coup sûr dans n'importe quelle
vidéo. On parle de "tracking", voire de "problème général du tracking".
Initialement je suis parti de la thèse de
Sylvain Boltz. Il s'agissait de retrouver un bout d'image, appelé aussi "modèle
d'apparence", dans une autre à l'aide d'une mesure de dissimilarité particulière basée sur les "k plus proches voisins" (kPPV ou kNN en anglais
pour "k-nearest neighbors"). Ceux-ci collent bien aux "densités locales", même en "dimension élevée" (contrairement aux
fenêtres de Parzen qui elles souffrent du
fléau de la dimension), ce qui est toujours le cas avec des vidéos.
Les kPPV permettent d'élaborer une
divergence de Kullback-Leibler très intéressante pour comparer deux
images ou vidéos. Celle-ci conduit en effet à des bassins de convergence plus "lisses" et "localement" plus "convexes" que ceux issus d'autres
métriques plus classiques (SAD, SSD, ZNCC, BAT, etc.). À données égales les chances de converger augmentent donc.
Au passage, on note que toutes ces mesures s'intègrent aussi bien dans des schémas d'optimisation (type
mean-shift) que de filtrage (type filtre à particules). Ces deux catégories
peuvent sembler opposées mais seul l'"étiquetage spatio-temporel" de leurs cibles change. Tantôt la piste
est perçue de façon "nette" (optimisation ~> étiquetage "dur", par exemple [0 0 1]) tantôt de façon "diffuse" (filtrage ~> étiquetage "doux", par
exemple [0,3 0,1 0,6]). Pour revenir aux travaux de S. Boltz (en "tracking"
uniquement) malheureusement de très nombreuses questions débordent du seul paramétrage de la cible et de la métrique employée pour effectuer des
comparaisons (aussi pertinents que soient les kPPV !). En voici un florilège :
Tout d'abord dans le cadre de la "modélisation non paramétrique" (ce qui était le canevas de ma thèse). Quid de l'antagonisme "ROI" / "non ROI" (i.e.
entre ce qu'il y a à l'intérieur et à l'extérieur de la zone d'intérêt), du choix
des espaces de description des pixels (XYRGB ou XYGxGy ? et pourquoi pas XYVT ?), quid du choix des pixels eux-mêmes (ce qui peut se ramener à la
forme de la zone d'intérêt), quid des pondérations des dimensions (uniforme au début mais rarement ensuite...), quid de l'aspect "hétéroclite"
d'avoir à gérer d'un côté un modèle d'évolution "paramétrique" (très) pauvre en degrés de liberté (ddl) (mais très utile pour "tuer le bruit" !) et
de l'autre un modèle d'observation "non paramétrique" (très) riche en ddl (mais très pratique pour éviter les "fausses interprétations" !). Imaginer
l'inverse s'avère d'ailleurs réjouissant (cela amène tout de suite à un problème de
"transport optimal" ! :O ;-) :$).
Hors de ce cadre ensuite. D'autres problèmes sautent aux yeux : quid si la caméra bouge elle aussi (perspective soit déprimante soit
réjouissante pour le thésard qui essaie de résoudre une bête question...), quid de la correspondances 2D/3D (intégration de la géométrie projective
basée sur l'hypothèse de rigidité des objets à suivre... vaste programme pour le néophyte !), quid du nombre d'entités mobiles (en gros de la
gestion de certains ddl), quid du paramétrage général du suivi (paramètres "tournevis" souvent cachés et figés dans l'optimisation ou le filtrage), quid
de l'évolution du modèle d'observation (cf. "apprentissage en ligne" / "online machine learning") voire du modèle prédiction aussi (pourquoi pas !?).
Bref, l'espace des possibles est immense (et donc démoralisant quand se cantonne plus d'un an dans une petite case qui s'avère minuscule
rétrospectivement... Pour moi la case était : suivi 2D, ROI rectangulaires, filtre à particules
MCMC et représentations de type XYRGB) d'autant que mes essais échouaient facilement... Il est toujours long de désacraliser ce qu'on a
(trop !?) sacralisé ! Fort heureusement cela m'a conduit à prendre beaucoup de recul.
D'abord (2ème année) j'ai voulu comprendre les différences entre modèles non-paramétriques (comme les données d'une image ou les signatures
d'un descripteur) censés "rester fixes" et modèles paramétriques (comme les transformations géométriques) censés "varier" uniquement sur leurs
"degrés de liberté". Au fil du temps, je me suis aperçu que ce problème (Qu'est-ce qui bouge ? Qu'est-ce qui ne bouge pas ?) était extrêmement
mal traité (car non posé) dans "le domaine" (ce qui me désole mais me permets aussi de relativiser). Or je pense que cette question doit être
rigoureusement posée (et un jour traitée !) par les mathématiques. Mais, je l'avoue honteusement, ce n'est pas à ma portée... Je suis un
expérimentateur, pas un théoricien... Ne comptez pas sur moi pour passer par la face nord. J'emprunterai la face sud ! En effet, depuis,
je "vois" un lien indiscernable entre "degré de liberté" et "support
associé" (et je suis désormais "choqué" par l'arrivée ex-nihilo de certains ddl dans la résolution d'un problème ! Pour moi la "vraisemblance" ça se
mérite ! Et pour résumer, donc, il devrait y avoir "autant de raisons de douter de nos représentations que de nos observations". Ceci revient
à dire qu'à l'origine, il ne peut y avoir "intrinsèquement" qu'un "énorme doute, absolu et uniforme". Partout... Bon, cela frise la mystique mais ce
n'est pas du tout déconnant. Cela colle même avec énooooooormément de choses (on n'imagine pas !). Au fil de ces réflexions, je me suis passionné du
coup pour la "théorie de l'information" ("Le bazar, ça se mesure !"). Suivant
cette interprétation, j'ai été fasciné par le parallèle qu'on pouvait établir entre l'inpainting (une technique de reconstruction numérique) et l'illusion
de la tâche aveugle, un phénomène bien connu depuis 1660 grâce à Edme Mariotte. Le credo est très simple : "maintenir coûte que coûte l'entropie - i.e.
l'information - constante !". Personnellement, cela a été un vrai choc. D'abord parce que cela bat en brèche le 2nd principe de la thermodynamique,
censé toujours accroître le bazar (oui oui !). Ensuite parce que cela montre - a contrario de ma quête de simplicité (type
MDL) - que trop réduire l'entropie conduit toujours à une erreur fatale : radoter !
Et donc se fermer à la nouveauté... Cela m'évoque aussi la "quête de l'invariance", même si c'est un peu différent, tant en géométrie projective (isométries,
etc.) qu'ailleurs (mécanique, relativité,... physique quoi !). Depuis, j'ai cherché à voir toutes les illusions d'optique inventoriées à ce jour. Deux
m'intéressent tout particulièrement. Elles semblent étayer l'idée qu'"il est extrêmement efficace de faire 'comme si' l'information se conservait
pour voir !" (mais il faudrait que je m'y remette... :S). Ensuite, j'ai gratté tout ce que j'ai pu en géométrie projective (mais cela n'était pas censé
faire partie de ma thèse... :S) pour m'approcher des verrous scientifiques actuels (vu que c'est la partie la plus aboutie du domaine). Enfin, je me suis
lancé dans une revue (loin d'être achevée...) de tous les schémas de tracking possibles en vision. À chaque fois le but est de cerner les hypothèses des
méthodes actuelles pour en comprendre les limites. À ce stade, je cherche à soulever des questions basiques comme :
La caméra qui filme bouge-t-elle, oui ou non ? Est-il nécessaire de la calibrer ? Quand le suivi 2D devient-il caduc ? Comment effectuer un suivi 3D
sur une séquence 2D lorsque non seulement la caméra bouge mais aussi les objets 3D ? Est-ce toujours possible ? Comment étoffer le modèle de référence ?
Comment se rendre compte que l'objet suivi reste rigide ? Combien de dégrés de liberté tolérer au maximum ? Et, de façon connexe, combien d'entités indépendantes
y associer au maximum ? Vaut-il mieux chercher un modèle d'évolution paramétrique ou un modèle d'observation non paramétrique ? En quoi sont-ils complémentaires ?
Quid si l'objet se casse ? Quid si l'objet s'avère être un fluide ? Que doit-on vraiment chercher/modéliser au final ? Quelles sont les hypothèses ultimes pour
pouvoir suivre/identifier n'importe quoi dans n'importe quelle situation avec une caméra ?
Voilà, je renvoie à ma page de recherche pour plus de détails. Comme ce sujet réclame un traitement
assez démentiel, j'essaierai de développer ici certains points au fil du temps (et surtout de proposer de longs articles). Quand, in fine,
j'estimerai avoir une solution élégante et générale alors je soutiendrai. Mais pas avant ! Voilà. Il est possible que ce jour n'arrive jamais
(mais si cela vous désole vous pouvez toujours m'aider : un simple mail me fera toujours plaisir !).
 $\hspace{100px}$
$\hspace{100px}$




